De middentoonstemming van het Hemony carillon


Voor de echte belangstellenden even een stukje muziektheorie. Maar pas op, het wordt ingewikkeld. In de eerste plaats, wat is geluid. Het geluid dat wij waarnemen wordt veroorzaakt door luchttrillingen. Voor wie niets weet van trillingen, kijk naar de slinger van een klok. In de uiterste stand links, is de snelheid nul. De slinger gaat terug naar het onderste punt, daar is de snelheid maximaal. Daarna gaat de slinger naar het uiterste punt rechts, de andere kant op dus, en daar aangekomen is de snelheid weer nul. In omgekeerde richting gaat het daarna verder. We kunnen dit proces weergeven met een slingertje, officieel een sinuscurve genoemd. Een complete trilling houdt, in termen van de klokslinger, in: een volledige heen en weer-gang van de slinger. Eén trilling per seconde wordt één hertz (Hz) genoemd. Meerdere trillingen per seconde (wordt genoemd de frequentie) ofwel zoveel hertz. 100 trillingen per seconde is 100 Hz.

De frequentie van onze wisselspanning is 50 Hz.


Muziek, ontdaan van gevoelsfactoren, is dus een ratjetoe van geluidsfrequenties.

De basis hiervan wordt gevormd door de toonladder: do, re, mi, fa, sol en zo voort. Of: C, D, E, F, G, A, B, C. (Waarom de toonladder niet met A begint maar met C komt, omdat de A de laagste en de hoogste toon in het notenschrift is. De C is het midden van de G (bassen) en de F sleutel (violen).


Was het maar zo eenvoudig, maar bij de noten van die toonladder hoort een frequentie. Het verschil tussen de tonen hangt af van de verhouding van de frequenties. En dan begint het probleem. (Nog erger, de muziekleer maakt gebruik van “cents”. Wat dat is, staat onderaan). Want we maken niet alleen gebruik van enkelvoudige noten, maar we gaan die ook combineren. Daarbij krijgen we te maken met intervallen. 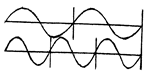Hieronder wordt verstaan de frequentie-verhouding van twee noten. Klinken die noten tegelijkertijd, dan spreekt men van een harmonisch interval. Klinken meerdere noten tegelijkertijd, dan heet dat een accoord. En dat moet liefst aangenaam klinken. In ideale vorm zogenaamd “rein”. Dat wil zeggen, dat de frequenties in de pas lopen.

Bij voorbeeld het octaaf. Het octaaf heeft de omvang van een complete toonladder en de frequentieverhouding bedraagt 1 :2. Daarnaast kennen we de kwint (de omvang van zeven halve noten) met een frequentie- verhouding van 2:3 en de grote terts (met een omvang van vier halve noten) en een frequentieverhouding van 4:5.Dit kan mooi weergegeven worden in een tekeningetje.




zo ziet een octaaf er uit.




zo een kwint





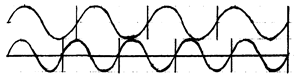
en zo de grote terts




Was het nu maar zo dat we vanuit iedere noot binnen het octaaf een reine grote terts of een kwint konden spelen. Een viool of menselijke stem kan dat wel, maar een piano of beiaard niet. Men heeft getracht hier een oplossing voor te vinden. Dit heeft geleid tot verschillende stemmingen. In de bijlage zijn van enkele stemmingen de frequenties van de noten uit één octaaf vermeld, uitgaande van de stamtoon A 440 H. Om uit de problemen te geraken heeft men een stemming ontwikkeld, namelijk de evenredig zwevende stemming, die, behalve het octaaf zelf, voor de rest van de noten een tikkeltje vals is, maar zo weinig dat haast niemand het hoort, maar waarop alles gespeeld kan worden. Zo is de piano gestemd en ook het Eysbouts carillon.

De frequentieverhouding van alle “halve” noten is ! gelijk en wel de twaalfde machtswortel uit twee. Of wel met een frequentieverhouding tussen alle “halve” noten van 1,059463094.


Het Hemony carillon is gestemd volgens de zogenaamde middentoonstemming.

Daarbij is getracht zoveel mogelijk grote tertsen “rein” te stemmen. Het klink bijzonder zuiver, alleen blijven er helaas enige intervallen over die zo vals klinken dat ze niet om aan te horen zijn. Ook is het Hemony carillon niet gestemd met de stamtoon A 440 H. In het tabelletje met de stemmingen is daar wel van uitgegaan, om der wille van de vergelijkbaarheid. Wie van rekenen houdt kan het narekenen. Gis -Dis’ tegelijkertijd geeft een verhouding van 1,5328 en dat is zo vals als roet. Muziek waarin dit interval voor komt kan op het oude carillon niet gespeeld worden. De Dis ontbreekt dan ook, evenals bij sommige oude orgels die ook nog in de midden_ stemming staan.


Om het nog moeilijker te maken moet er op gewezen worden dat er vrijwel geen instrumenten zijn die een enkelvoudige toon voortbrengen. Vrijwel altijd is er sprake van boventonen. Dit zijn tonen die tezamen het timbre van de klank vormen. Veelal zijn dit harmonische met een frequentieverhouding van 1 :2:3:4 enz. Bij strijkinstrumenten blijft het daartoe wel beperkt. Bij klokken,met hun gecompliceerde vorm, ligt dit ingewikkelder. Gewoonlijk is de verhouding van de eenvoudigste boventonen die van 1 :2:3 en dan nog meer, maar veel minder dominante tonen. Dit betekent dat naast de grondtoon (de 1) een toon die een octaaf hoger ligt (de 2) en een derde toon die een kwint daarboven ligt (de 3). Enz. Het blijkt dat niet de grondtoon, maar de toon een octaaf hoger, de slagtoon, domineert. Bovendien blijkt ook de kleine terts (omvang 3 halve tonen) dominant te zijn. Eysbouts heeft klokken ontwikkeld die niet deze kleine terts, maar een grote terts als dominante boventoon hebben.


In de Beiaardschool is er een aanwezig. Maar de beiaardiers vinden dit maar niks. Klokken met sterk dominerende hoge boventonen geven een “blikkerig” geluid. Overigens zijn er metingen uitgevoerd aan een bepaalde klok waarbij wel 17 boventonen vastgesteld zijn.


Noot:

“Cents” omvatten de frequentieverhouding van de twaalfhonderdste machtswortel uit twee. Ofwel 1 ,00057779


Bijlage:

Freqentietabel


Alle frequenties zijn afgerond op hele getallen. Er kunnen dus kleine verschillen optreden.


Zoals al eerder opgemerkt, geeft verdubbeling van de frequentie een toon die een octaaf hoger ligt. Halvering overeenkomstig een octaaf lager. De complete reeks van de stamtoon “A” ziet er als volgt uit: 27,5; 55; 110; 220; 440; 880; 1760; 3520; 7040; 14080. Hoger en lager hebben geen zin, die zijn door het menselijk oor niet waarneembaar maar zijn wel nodig voor de gevoelswaarde van de klank.


Bron: Jaap Vos, april 2002